
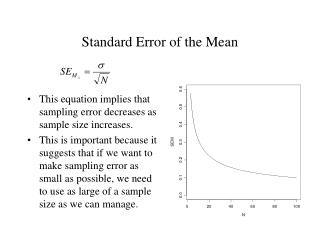
Starting with version 8.2, Prism will only show the SE if you request symmetrical confidence intervals. These are not computed from the SE values, so it makes no sense to report both the SE and the asymmetrical confidence interval. However, many of the uses of the formula do assume a normal distribution. This formula does not assume a normal distribution. We recommend reporting asymmetrical profile likelihood intervals, which are more useful. where is the standard deviation of the original distribution and N is the sample size (the number of scores each mean is based upon). These intervals are computed from the SE values, so it makes sense to display them. Starting with Prism 8.2, Prism will only compute and display the SE of parameters if you ask Prism (in the Confidence tab) to report symmetrical confidence intervals. Why doesn't Prism display SE values for my fit?
When the SE value is preceded by ~, the corresponding confidence intervals are shown as "very wide" with no numerical range (the range would be infinitely wide). The standard error of those parameters is not well defined. In other words, many combinations of parameter values lead to curves that fit equally well. (standard deviation Standard Deviation Standard deviation (SD) is a popular statistical tool represented by the Greek letter to measure the variation or dispersion of a set of data values relative to its mean (average), thus interpreting the datas reliability. But when the fit is 'ambiguous', changing other parameters can move the curve so it is near the data again. Changing the value of any parameter will always move the curve further from the data and increase the sum-of-squares. If a value is preceded by ~, it means the results are 'ambiguous'. Why is there a ~ symbol in front of some SE values? Standard deviations are calculated by dividing the sum of equal values by squares root of the number of mean measurements (and sometimes N being shown ). Prism (and most programs) calls that value a standard error, but some others call it a standard deviation. The standard error of a parameter is the expected value of the standard deviation of that parameter if you repeated the experiment many times. When applied to a calculated value, the terms "standard error" and "standard deviation" really mean the same thing. The SEM can be thought of as "the standard deviation of the mean" - if you were to repeat the experiment many times, the SEM (of your first experiment) is your best guess for the standard deviation of all the measured means that would result. The SEM tells you about how well you have determined the mean. The SD tells you about the scatter of the data. When you look at a group of numbers, the standard deviation (SD) and standard error of the mean (SEM) are very different. Both terms mean the same thing in this context.

Prism reports the standard error of each parameter, but some other programs report the same values as 'standard deviations'. 'Standard error' or 'standard deviation' ? The calculation of the standard errors depends on the sum-of-squares, the spacing of X values, the choice of equation, and the number of replicates. Otherwise, we suggest that you ask Prism to report the confidence intervals only (choose on the Diagnostics tab). If you want to compare Prism's results to those of other programs, you will want to include standard errors in the output.
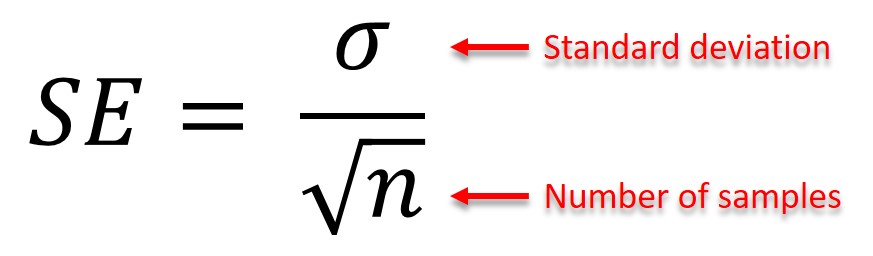
The only real purpose of the standard errors is as an intermediate value used to compute the confidence intervals. I don't know if there is an exact formula for the standard error but there is an asymptotic (in other words, approximate) one that is more complicated and more difficult to get and compute.Interpreting the standard errors of parameters If you were using the median instead of the mean to estimate the population median (which would not be wise for Normally distributed data as the mean is a better estimator for what is ultimately the same quantity the mean and the median are equal), you would have a different standard error, a larger one. At this point your estimate of the standard error is $\frac$, where $\sigma$ is the population standard deviation we use $s$ instead of $\sigma$ (usually presumed to be unknown) to estimate the standard error.


 0 kommentar(er)
0 kommentar(er)
